Abstract
A dimmer is an electronic device that controls alternate voltage applied to a lamp through delivering a selected portion of the mains sinusoid. Engineer, designing a dimmer needs to estimate how big this portion should be to get a desired luminance level. This article uses a model of incandescent lamp, tungsten resistivity, and human eye spectral efficiency to derive dependency of produced luminous flux over the voltage, gives a simple analytical function that describes this dependency with good accuracy (±2% comparing to the model).
Download PDF version of this article
Structured Abstract
|
Purpose |
To discover a dependency of luminous flux produced by an incandescent lamp on the applied voltage |
|
Methodology/Approach |
Numerical analysis on a theoretical model of an incandescent lamp |
|
Findings |
Analytical function for approximate estimating of luminous flux for the applied voltage with ±2% accuracy |
|
Research limitations/implications |
Model does not encounter thermal conduction and convection in the lamp. |
|
Practical implications (if applicable) |
Provided function has some degree of dependency on the lamp’s design (namely, nominal filament temperature) |
Definitions
Process of controlling some output value (such as voltage U or luminous flux L) we will denote as a control function ![]() , defined on the control parameter
, defined on the control parameter ![]() :
:
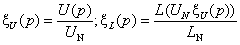 |
(1) |
Each of ![]() monotonously increase on the defined range. Control functions defined on a different (other than
monotonously increase on the defined range. Control functions defined on a different (other than ![]() ) argument we will denote in this article as
) argument we will denote in this article as ![]() .
.
Commonly used are linear (![]() ) and logarithmic (
) and logarithmic (![]() ) control functions. To implement a desired control function
) control functions. To implement a desired control function ![]() , we needs to know what is
, we needs to know what is ![]() dependency.
dependency.
The following chapters give an attempt to derive ![]() using a model suggested in (Agraval 1996).
using a model suggested in (Agraval 1996).
Incandescent Lamp Model
An incandescent lamp is characterized with few nominal values: PN – power consumption, UN – nominal voltage, LN – nominal luminous flux, produced by the lamp at nominal voltage. The flux is produced by filament, incandesced to nominal working temperature TN.
When lower voltage U<UN is applied, operating temperature T of filament is lower TN and therefore it produces less luminosity L.
Filament Resistance
Power, consumed by a lamp, is expressed with Ohm low:
| (2) |
where ![]() defines dependency of filament resistance over the temperature relatively to its nominal resistance RN, which can be evaluated via PN and UN:
defines dependency of filament resistance over the temperature relatively to its nominal resistance RN, which can be evaluated via PN and UN:
| (3) |
Dependency ![]() for tungsten is not linear in the working range of temperatures (1000-2500K). For this model we will use polynomial approximation of tungsten resistance ρ, [Harang 2003]:
for tungsten is not linear in the working range of temperatures (1000-2500K). For this model we will use polynomial approximation of tungsten resistance ρ, [Harang 2003]:
| (4) |
![]() can be expressed via
can be expressed via ![]() as the following:
as the following:
| (5) |
Filament Temperature
During operation, filament radiates electromagnetic energy and dissipates heat via conduction and convection. To estimate radiation, filament is modeled [Agraval 1996] as a simple non-ideal blackbody that obeys Plank’s radiation law:
 |
(6) |
where ![]() is power radiated between wavelength
is power radiated between wavelength ![]() and
and ![]() ,
, ![]() – tungsten emittance, and A is filament area. The total power emitted over all wavelengths is:
– tungsten emittance, and A is filament area. The total power emitted over all wavelengths is:
| (7) |
where σ is the Stefan-Boltzman constant and ![]() is average emittance over all wavelengths, which is approximated as a second order polynomial (Harang 2003):
is average emittance over all wavelengths, which is approximated as a second order polynomial (Harang 2003):
| (8) |
In a steady-state operation, power applied to the lamp is in balance with power radiated and dissipated to outside ambient. Dissipation has two constituents – conduction and convection. Agraval in [Agraval 1996] has suggested a reasonable way of accounting dissipation as a factor of input power:
| (9) |
Solving (8) for P:
| (10) |
Substituting left side of (10) with right side of (2):
| (11) |
Using (11), we may derive ![]() :
:
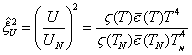 |
(12) |
Figure 1 illustrates dependency ![]()
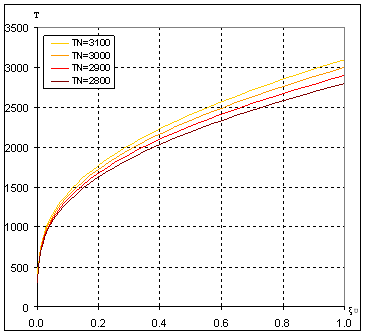
Figure 1. Dependency of T on fraction of applied voltage ξU for different TN
Luminance
Not all power radiated by filament has its effect on luminous flux. Some of the energy is absorbed by bulb glass and dissipated as heat. Although, this absorption depends on λ, we will simplify this absorption to a constant factor η<1.
Major part of the emitted energy is not visible to human eye. This is described as spectral efficiency function S(λ), approximated as the following [Agraval 1996]:
| (13) |
Thus, total luminous flux produced by a lamp can be defined as:
 |
(14) |
where
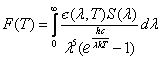 |
(15) |
Thereby, control function ![]() can be expressed as a function of T:
can be expressed as a function of T:
| (16) |
For working range of temperatures and visible area, emissivity є(λ,T) can be approximated as the following [Larrabee 1957]:
 |
(17) |
where T is in °K and λ in nm. Substituting (17) in (16) and integrating numerically (16) we get dependency, shown on Figure 2:
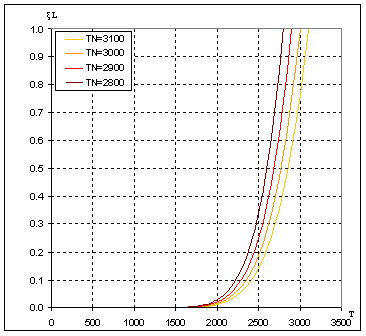
Figure 2. Dependency ξL(T) for different TN
Solving Luminance vs. Voltage
Using T as a parametric variable, we may numerically compute (11), (15) and graphically solve dependency ξL(ξU), as shown on Figure 3:
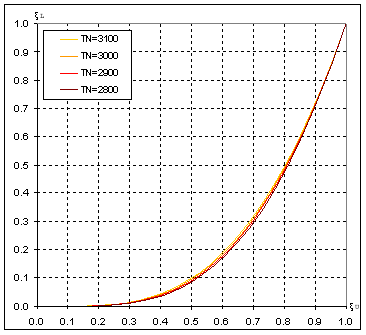
Figure 3. Dependency ξL(ξU) for different TN
As Figure 3 indicates, ξL(ξU) is affected by a design factor – nominal temperature TN.
Approximation
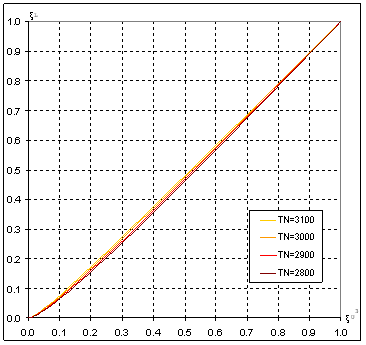
Figure 4. Dependency ξL(ξU3)
As it appears (see Figure 4), dependency ξL(ξU3) looks quite linear for ξU3>0.2 and has some higher-order dependency for ξU3<0.2. Therefore we will try approximating ξL(ξU) as two polynoms:
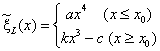 |
(18) |
Value ξLat x=1 is equal to 1 by nature of ξ, therefore c can be expressed via k:
| (19) |
To solve a and x0 we will require continuality of ![]() and its derived function
and its derived function ![]() , this gives us two equations with three unknowns:
, this gives us two equations with three unknowns:
 |
(20) |
Solving (20) for a and x0 we get them expressed via k:
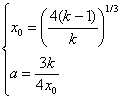 |
(21) |
Thereby, ![]() depends on a single constant k, which is then wiggled around to find a value giving lowest RMS deviation
depends on a single constant k, which is then wiggled around to find a value giving lowest RMS deviation ![]() . Table 1 lists selected values for few most common nominal temperatures TN, Figure 5 illustrates this dependency, and Figure 6 shows modeled curves and values, approximated with (20).
. Table 1 lists selected values for few most common nominal temperatures TN, Figure 5 illustrates this dependency, and Figure 6 shows modeled curves and values, approximated with (20).
Table 1. k values for some TN
|
TN |
k |
|
2800 |
1.067 |
|
2900 |
1.054 |
|
3000 |
1.043 |
|
3100 |
1.034 |

Figure 5. k variations over TN
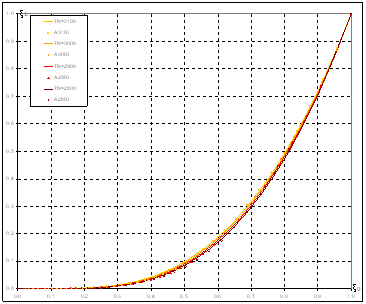
Figure 6. Modeled curves and approximated values (marks)
Since designer of a dimmer may not exactly know nominal temperature of the dimmed lamp, kcan be selected for an average nominal temperature. Suggested value k=1.05 gives ±2% error (against the model) for TN in range 2800-3100 °K. For this k, equation (20) becomes practically concrete:
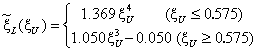 |
(22) |
Sine Wave Dimmer
A sine wave dimmer implemented with pulse-width modulation controls applied voltage with a cycle duty, which we will denote as control function ξt. Modulation frequency is usually chosen much higher than mains frequency. Therefore, RMS of output voltage is proportional to cycle duty, and control function ξU as simple as:
| (23) |
To make ξL(p), linear on parameter p, function ξt(p) should be defined as the following:
| (24) |
Applying (24) to equation (22) we get
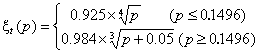 |
(25) |
Phase Control Dimmer
When implementing an AC dimmer based on phase control technique, one needs to tabulate cycle duty values ti as a function of desired luminance level pi.
Following the same approach, we introduce control function ξt:
| (26) |
where t is cycle duty (time when the switch is on) and tM is the mains half period, and f is the mains frequency. Average power ![]() applied to the lamp, can be evaluated as the following:
applied to the lamp, can be evaluated as the following:
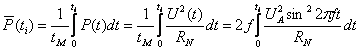 |
(27) |
where UA is voltage amplitude. Integrating (27) we can define ξP as the following
| (28) |
Considering that ![]() , and substituting (28) to (22) we may estimate
, and substituting (28) to (22) we may estimate ![]() .
.
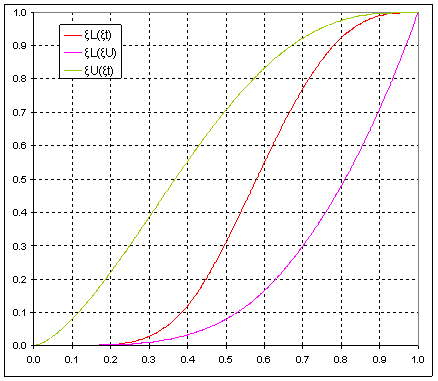
Figure 7. Dimmer control functions ξL and ξU
Applying approach used in (24) function ξt(p) is defined as following:
| (29) |
Although, reverse function of (28) is not solvable analytically, it can be solved numerically.
Conclusions
As a result of numerical modeling, the following approximation functions are suggested:
- Estimation of produced luminous flux over the voltage:
L = L0 * ((U/U0 < 0.575) ? 1.369 * (U/U0) ^ 4 : (1.05 * (U/U0) ^ 3 - 0.05);
- Tabulation of cycle duty over the control parameter p
t = (p < 0.1496) ? (0.925 * (p) ^ -4) : (0.984 * (p + 0.05) ^ -3);
References
Agraval D.C., Leff H.S., Monon V.J. (1996)
"Efficiency and efficacy of incandescent lamps"
American Journal of Physics, May 1996, Volume 64, Issue 5, pp. 649-654
http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=AJPIAS000064000005000649000001&idtype=cvips&gifs=yes
Harang O., Kosch M. J. (2003) "Absolute Optical Calibration Using a Simple Tungsten
Bulb"
Sodankylä Geophysical Observatory Publications, 2003, pp. 92:121-123
http://spaceweb.oulu.fi/28AM/proc_papers/27_harang_et_al_calibration_with_tungsten_bulb.pdf
Larrabee R.D. (1957) "The spectral emissivity and optical properties of tungsten"
Research Laboratory Of Electronics, Massachusetts Institute of Technology
http://dspace.mit.edu/bitstream/1721.1/4755/1/RLE-TR-328-04734719.pdf
Post a Comment